Langzeit: Regression
Jump to navigation
Jump to search
Zur deutschen Hauptseite | Alle deutschsprachigen Seiten
Im Referenzdokument MCP - Measure-Correlate-Predict - An Introduction to the MCP Facilities in WindPRO, Kapitel 2 wird die statistische Methode hinter Regressions-MCP erläutert. Die folgende Seite geht auf die Eingabeoptionen der Implementierung in windPRO ein.
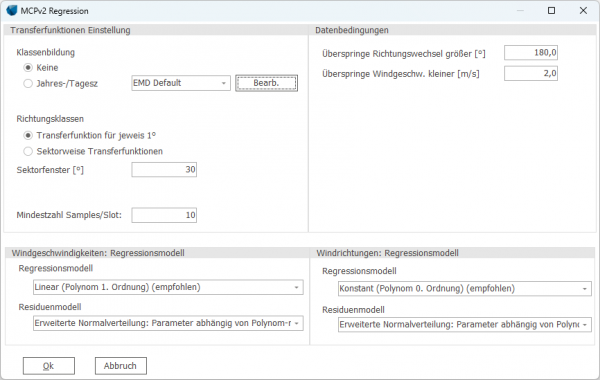
MCP-Modul → Session öffnen → Register Modelle LZ → Bearbeiten neben Zeile Regression
- Klassenbildung
- Standardmäßig wird keine Klassenbildung (außer Richtungen, s.u.) vorgenommen. Optional kann eine Klassenbildung nach Jahres- und/oder Tageszeit vorgenommen werden. Die Zeiten werden über die windPRO-Jahreszeiten/Tag-Nacht Einstellungen vorgegeben. Wird nur eine Tag/Nacht-Einteilung gewünscht, so sollte die Anzahl der Jahreszeiten auf 1 gesetzt werden. Es wird empfohlen, die Anzahl der Jahres- bzw. Tagesperioden gering zu halten (z.B. nur Tag/Nacht und Sommer-/Winterhalbjahr), da ansonsten die Gefahr besteht, dass es pro Klasse so wenig Daten gibt, dass das Ergebnis nicht mehr repräsentativ ist.
- Richtungsklassen
- Transferfunktionen können entweder jeweils für einen Sektor (also i.d.R. 12 Transferfunktionen) oder für jeweils 1° (also 360 Transferfunktionen) ermittelt werden. Da das Ergebnis bei gradweisen Transferfunktionen exakter ist, ist dies die voreingestellte Methode. Das sektorweise Vorgehen ist der gängige Weg bei selbst gemachten Tabellen und kann z.B. ausgewählt werden, wenn WindPRO MCP2005 mit einer solchen Tabelle verglichen werden soll.
- Sektorfenster
- Ist die Option Transferfunktionen für jeweils 1° gewählt, reicht in der Regel die Menge an Samples pro Grad nicht aus, um daraus repräsentative Transferfunktionen zu berechnen. Deshalb wird standardmäßig ein Sektorfenster von 30° verwendet, also die Richtung +/- 15°. Für die Richtung 23° werden also z.B. alle Datensätze zwischen 8° und 38° verwendet. Wenn ein Sektorfenster von 360° gewählt wird, wird nur eine einzige Transferfunktion, die auf allen Daten beruht, erstellt.
- Überspringe Richtungswechsel größer...
- Insbesondere bei niedrigen Windgeschwindigkeiten kann die Windrichtung zwischen Langzeit-Referenz und Standortdaten beträchtlich variieren und der Korrelation eine Menge statistisches Rauschen hinzufügen. Durch das Ignorieren von Daten mit großen Richtungswechseln kann dieses Rauschen reduziert werden. Dies bedeutet allerdings, dass eventuell wichtige Informationen verworfen werden. Voreinstellung ist, dass alle Daten verwendet werden (Richtungswechsel >180° existieren nicht).
- Überspringe Windgeschwindigkeiten kleiner...
- Bei geringen Windgeschwindigkeiten ist eine lineare Beziehung zwischen Standort und Referenz, die bei höheren Windgeschwindigkeiten deutlich hervortritt, häufig nur sehr schwach ausgeprägt. Deshalb tragen niedrige Windgeschwindigkeiten oft trotz ihrer geringen Relevanz viel statistisches Rauschen zur Regression bei. Abhängig von der Breite der Streuung und der tatsächlichen Windgeschwindigkeiten kann dieser Wert frei definiert werden, voreingestellt ist ein Wert von 2 m/s.
- Das Überspringen der Windgeschwindigkeiten bezieht sich nur auf die Referenzdaten und nur auf die Ermittlung der Transferfunktion, nicht auf deren Anwendung bei Erstellung der Langzeitreihe.
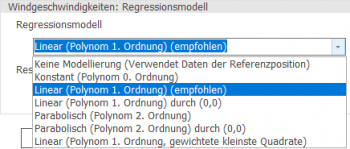
- Regressionsmodell (Windgeschwindigkeit)
- Hier wird die Art der Regression für die Windgeschwindigkeit ausgewählt. Lineare Regression bedeutet eine Regression erster Ordnung, wobei eine freie Regressionsgerade derjenigen durch den Ursprung (0,0) gegenüber zu bevorzugen ist, da sie in der Regel in dem Windgeschwindigkeits-Bereich, der für die WEA-Produktion relevant ist, eine bessere Anpassung bietet. Alternativ kann eine Regression 2. Ordnung gewählt werden, die eine Parabelförmige Regressionskurve ermittelt. Achtung: Dies mag zwar zu einer besseren Anpassung führen, kann aber auch zur Folge haben, dass extreme Windgeschwindigkeiten die Anpassung bei den hohen Windgeschwindigkeiten beeinträchtigen.
- Regressionsmodell (Windrichtung)
- In der Regel sind Wechsel der Windrichtung unabhängig von der Windgeschwindigkeit, deshalb sollte eine Regression 0. Ordnung verwendet werden (d.h. eine waagrechte Regressionsgerade). Die zur Wahl stehenden Modelle entsprechen denen zum WG-Regressionsmodell (siehe Grafik oben)
- Residuenmodell (Windgeschwindigkeit und Windrichtung)
- Voreinstellung für die Windrichtung und die Windgeschwindigkeit ist die Erweiterte Normalverteilung mit Polynom-modellierter Windgeschw. (Ordnung:1) mit der Regressionsformel: y = ax + b + e(x). Die Spanne der Windgeschwindigkeiten wird in eine Anzahl Intervalle aufgeteilt. Innerhalb jedes Intervalls wird die Streuung anhand ihrer Standardabweichung und der Abweichung des Mittels (relativ zur Regressionsgeraden) charakterisiert. Diese beiden Charakteristika werden als Zufallselemente (oben: e(x)) dann auch auf die erzeugte Zeitreihe angewandt, um die nicht-lineare Zunahme der Windenergie mit der Windgeschwindigkeit besser abzubilden. Die beobachtete Standardabweichung wird als Polynom erster Ordnung modelliert.
- Für die Windgeschwindigkeit sollte die Methode Keine Modellierung im Normalfall nicht verwendet werden. Da die Windenergie nicht linear mit der Windgeschwindigkeit zunimmt, die Regression aber auf Basis der Windgeschwindigkeiten durchgeführt wird, führt dies häufig zu einer Unterschätzung der Windenergie. Die Einstellung Keine Modellierung hat eine Berechtigung, wenn die resultierende Zeitreihe keine Zufallsstreuung enthalten darf, z.B. da sie in PERFORMANCE CHECK mit SCADA-Produktionszeitreihen abgeglichen werden soll.
- Die Methode Normalverteilte Residuen ist veraltet, ist jedoch aus Kompatiblitätsgründen weiterhin verfügbar. Sie nimmt an, dass die Spannweite der Streuung in der Regressionsgrafik bei allen Referenzwindgeschwindigkeiten gleich ist und dass das Zentrum der Streuung die Regressionslinie sein musste. Die Transferfunktion wird damit zu y = ax + b + e. Die Anwendung dieser Methode auf Datensätze mit schlechter Korrelation oder ungleichmäßig verteilter Streuung kann zu Fehlern führen, häufig zu einer Überschätzung.
- Die Erweiterte Normalverteilung mit Polynom-modellierter Windgeschw. (Ordnung:2) hat häufig das Problem, dass wenige verstreute Punkte bei hohen Windgeschwindigkeiten die simulierte Streuung in die Höhe treiben können. Es wird deshalb empfohlen, diese Methode vorsichtig einzusetzen und im Zweifelsfall die Standardmethode zu verwenden.
Weiter mit:
- MCP-Überblick
- Die MCP-Session
- Register Zeitreihen
- Register Einstellungen Session
- Register Justierung
- Register Modell-Input
- Register Konzept-Wahl
- Register Modelle LZ
- Register Lokal skaliert
- Session-Überblick
- MCP-Berichte
- MCP-Modelle