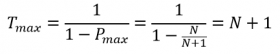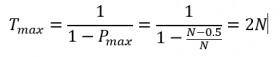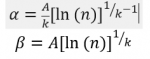Lasten - Anhang I: Gumbel Theory of Extremes and more

Zur deutschen Hauptseite | Alle deutschsprachigen Seiten

Emil J. Gumbel’s model of extremes published in “Statistics of Extremes” in 1958 is the classical standard model for describing the statistics of extreme events. The model is also called Fisher-Tippett Type 1 asymptote or Generalized Extreme Value model (GEV) type 1. The Gumbel model describes the distribution function of annual extremes, i.e. the cumulative probability, G(u), that a yearly maximum wind speed of u is not exceeded and takes the form:

Where the parameters β and α, are called mode and dispersion or sometimes location and scale.

There is a simple relation between the Gumbel distribution of annual extremes and the cumulative mean distribution of all wind speeds samples, F(u). The mean distribution, also called the parent distribution, is typically assumed to be Weibull. The simple relation states that the probability that a given extreme wind speed is the largest among N samples is given as the cumulative parent distribution multiplied by itself N times. For large N the exact distribution of annual extremes converges asymptotically to the Gumbel distribution:

The error of using the Gumbel asymptote is related to the number of independent samples in a year as well as the k-parameter of the Weibull parent distribution (i.e. the tail behaviour). For lower k-parameters the rate of convergence (i.e. more accurate already for small N) is much faster than for higher k-factors. It is also important to note that all N samples are assumed to be independent, i.e. not correlated. In real life this is not the case for all 10-minute or hourly wind speed samples in a year. The demand for independence leads to considerable complexity. Thus, usually the Gumbel distribution is not estimated from the parent distribution, but rather, directly from extracted extreme samples of the time series and then combining these with theoretical estimates of the cumulative probability of non-exceedance (P_i≈G(u_i)) called “plotting positions”. A Gumbel distribution is then fitted to (u_i, Pi) to obtain the Gumbel distribution parameters, α and β.

In the original Gumbel approach the annual maximum samples (u_i) are extracted for each year of an N year time series. These extreme samples are then ranked (i) smallest to largest (i equals 1 to N) and attributed the plotting positions, Pi, the theoretical estimates of the cumulative distribution function, approximating the probability that the annual maximum wind speed u_i is not exceeded. Several formulas for plotting positions have been suggested. The original Gumbel formula is:

which in fact was introduced by Weibull (Makkonen, 2004).

An alternative plotting position is due to Hazen (Makkonen, 2004), which is used in the extreme wind plots in for example, most Risø/DTU software (e.g. WAsP Engineering):

The extreme wind speed samples, u_i, are then plotted on the x-axis versus a transform of the chosen P-values, called the reduced variate, y:

With this transform the Gumbel asymptote takes a very convenient linear form:

Thus, a linear fit to a plot of (u_i, y_i) provides the parameters of the Gumbel distribution.

The IEC design criterion for extreme wind speed is a 50-year event, where “50” is referred to as the return period. In other words the design criterion is the wind speed that is expected to occur only once in 50 years. The return period is related to the annual risk of exceedance (R) via:

Thus, for T=50 years the annual risk of exceedance is R=2%, which is a much more stringent and basic definition of the design criterion than “50 years return period”.

Once the Gumbel parameters, α and β, have been obtained from a linear fit to (u_i, y_i) the extreme wind estimate for T=50 years (i.e. R=2%) may be obtained from:

Where y(T=50) equals 3.9. Thus, to obtain the estimate of the 50-year wind speed, the linear Gumbel fit of (u_i, y_i) must be extrapolated to y=3.9.

Implicit assumptions in the choice of "plotting positions"

The plotting position associated to each of the extracted extremes is a theoretical estimate of the annual probability that this wind speed is not exceeded. As such this probability also implies an assumption of the return period of the highest of the extracted wind speeds.

For the classical Gumbel plotting position the max wind speed extracted is assumed to have a return period of:

Using the Hazen plotting positions the same max wind speed is assumed to have the return period:

As example with 10 years of data (i.e. N=10) employing the classical Gumbel plotting positions relies on the assumption that the overall maximum wind speed recording has a return period of 11 years. For the Hazen plotting positions the assumed return period is 20 years. A more extreme example is a time series of 25 years. Using the Hazen estimates assumes the max recording to have a return period of 50 years. Thus, it is obvious that the Hazen plotting positions are much less conservative than those of the classical Gumbel method.

Extreme wind speed estimate at return period 1 year

The IEC standard also mentions that the extreme wind speed for T=1 year must be estimated although it is not used directly in the extreme wind check. However, the exact expression above for y(T) is not defined for T=1 year. Instead the most likely extreme to encounter any given year is usually chosen as the most appropriate estimate; this value equals the mode of the Gumbel distribution, i.e. the parameter β from the linear fit (which does not exactly equal the mean as the distribution is not symmetric). So we employ the definition of the extreme wind estimate with return period of 1 year as:

This definition is consistent with the equation derived using a Poisson process (see for example ).

Fitting the Gumbel asymptote

The linear fit to (u_i, y_i) described above represents is the basis of Gumbel’s asymptotic model of extremes. However, this linear fit may be performed in various ways. Firstly it is worth noting that the fit is performed on (u_i, y_i), i.e. with the reduced variate as the dependent variable. The reason for this is the implicit assumption in the standard least-squares fitting routine that the dependent variable (here, y) has much higher uncertainty than the independent one (u). The argument is that the wind speeds are measured using high quality equipment whereas y (reduced variate) is a transform of a theoretical estimate of the annual probability of each wind speed not being exceeded, which is associated with considerable uncertainty.

The standard fit is performed using the least-squares method. Monte Carlo simulations (not published) have shown that typically this fit introduces a slight conservative bias.

An alternative fit is done using the Probability Weighted Moments, PWM (Abild, 1992) which only takes the ranked wind speeds as input, and, hence, does not utilize the reduced variate. In this way the PWM fit avoids the main source of method-induced bias. The PWM expressions for the fit parameters to the Gumbel asymptote, scale (α) and location (β) are:

and

With estimates of the sample probability weighted moments given as:

and

Monte Carlo simulations (not published) have shown that the PWM fit to the Gumbel asymptote does not introduce a bias in the Gumbel fit. Unfortunately, the PWM fit does not work equally well with all the ways of extracting the extreme samples. It seems that PWM only is only bias-free for the traditional Gumbel approach where only the annual extremes are extracted.

Annual maximum method (AM)

The traditional Gumbel method only extracts the most extreme sample of each year, or from alternatively the most extreme sample of each period of fixed length sub-dividing the time series. Hence, the method is referred to as the Annual Maximum method (AM) or Periodical Maximum method.

The drawback of the AM method is the requirement of relatively long time series for the fit to the Gumbel asymptote to be meaningful. Typically, at least 5-10 years is recommended to constrain the fit parameters reasonably well.

In SITE COMPLIANCE at least 5 years of data are required for the AM method to be available.

Fit

The PWM fit is used with the AM method as it guarantees the least bias in the fitting. Since the PWM fit does not require plotting positions no Gumbel plot is needed. But is used for visual presentation, however.

Peak-Over-Threshold method (POT)

In some applications this method is also referred to as method independent storms. In most applications 5-10 years of on-site measurements are rarely available and within each year there may be more than one significant storm event. Hence a group of extreme wind methods have been developed which utilize more than a single storm from each year. These methods are referred to as Peak-Over-Threshold methods. Storms are typically extracted by defining a high threshold to select only high wind events which exceed this threshold. To ensure that the storm events are statistically independent events a minimum time difference is required between the extracted events, typically a few days. The extracted extreme samples may then be analysed in a way very similar to that of the standard AM Gumbel approach.

Normally, the recommendation for POT methods is given as the number of events to be extracted as 20-50 extremes. This makes the selection of a proper threshold an iterative procedure. As a more efficient way of extracting the extreme samples in SITE COMPLIANCE we have introduced a variation of the POT method which we call POT-N. Instead of defining a threshold the wished number of extremes is defined directly and the program then internally selects the proper threshold to obtain this number of extremes.

As in the AM method the extracted extreme samples are ranked and the “plotting position” (Pi) is attributed to each of the extracted extremes, i.e. the theoretical estimate of the probability of not being exceeded. For POT-N we have decided to use the classical Gumbel plotting positions in SITE COMPLIANCE

Instead of a “storm rate” of just one storm/year as in the AM method the storm rate is λ storms/year in a POT-estimation. Thus, a direct Gumbel fit to the extracted extremes would not yield the distribution of annual extremes, but simply the distribution of the extracted storms. To compensate for this the plotting positions, Pi, may be raised to the λth power provides an estimate of the PDF of the annual extremes. This transformation is equivalent to a simple shift on the y-axis, i.e. the standard reduced variates are shifted by ln(λ):

After this transform the POT Gumbel plot is fully equivalent to the AM plot, with y__annual=3.9 for T=50 years.

Fit

Our studies have shown that the PWM fit does not work well for the POT method as for the AM, unfortunately. Instead, a linear leat squares fit to the (u,y) is used. The classical Gumbel plotting positions are used as the implicit assumption of return period of the max wind recording seems more sensible than for the Hazen plotting positions.

Weibull parent (EWTS/Bergström) method

The occurrence of high extreme events is closely linked to the tail behaviour of the wind speed distribution. The heavier the tail the more likely are high extreme events to occur. For Weibull distributions commonly adopted in wind energy the shape of the tail is determined by the Weibull shape or k-parameter. A lower k-parameter means a heavier tail and that extreme events are more likely.

This effect has been quantified in the European Wind Turbine Standard (EWTS) that includes a method for extreme wind estimation based on the “Parent”-distribution in this case the Weibull distribution. The method simply assumes a universal number of independent extremes per year (N). The so-called “exact distribution” of the annual maximum is then obtained by raising the Weibull cumulative distribution function to the power of this number, N.

There is an error in the EWTS publication in the number of independent samples which they set to 23037 per year with reference to Bergström (1992). However, there the correct number for 10-minute data is n=2302 independent samples per year, or around every 20^th 10-minute sample. For hourly-averaged data the number is 883 or approximately every 10^th hourly sample. The error arises due to an exponent of effective frequency which is incorrectly transferred a factor of 10 in EWTS.

The slope and offset of the Gumbel asymptote (for high n) to the “extracted distribution” of annual extremes are given as (Bergström, 1992, EWTS, 1998):

The difference between the “exact” and Gumbel asymptote is not significant, and working with the Gumbel asymptote allows a fully consistent plotting with the other extreme wind estimation methods.

Omni-directional or sector-wise

The EWTS/Bergström method requires omni-directional Weibull parameters. In the WAsP context Weibull parameters are sector-wise, which is much more realistic and allows for multimodal omni-directional total distribution (several peaks). However, an omni-directional Weibull distribution called “Combined” may be estimated from the sector-wise Weibulls according to the method in the European Wind Atlas.

Fit - is the WAsP Weibull fit appropriate for extreme wind estimation?

The WAsP-type Weibull fit, fits exactly the third moment (energy) and frequency above the mean speed of the table data (no power curve or truncation is applied). Thus, the WAsP fit has a very strong emphasis on the tail behaviour. This is in contrast to ordinary least-squares or maximum-likelihood fits, that fit the wind speeds (and not the energy). These fits tend to fit well around the mean where the highest frequencies of occurrence are, at the cost of reproducing the tail behaviour less well. In conclusion, the WAsP Weibull-fit is in fact better than most other fits at reproducing the right tail behaviour, which is of main importance in extreme wind estimation.

Preconditioning

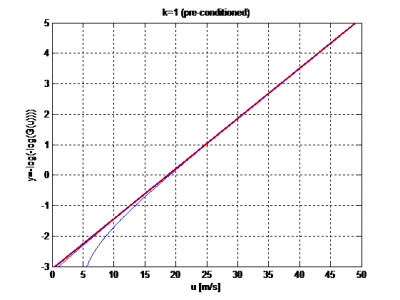
The Gumbel distribution is an asymptotic distribution. As the number of independent (i.e. not correlated) samples in the pool from which the extremes are extracted, e.g. 1 year, approaches infinity, the Gumbel asymptote becomes exact. The accuracy of the asymptotic assumption depends on the number of independent samples but also on the shape of the parent distribution, i.e. the Weibull distribution. For a k-parameter of 1, the convergence is extremely fast and the asymptote practically exact for just few samples. For higher k-factors the convergence is much slower (see Cook, 1982).

The deviation of the true annual extreme distribution from the Gumbel asymptote is a slight curvature of the extreme samples when plotting the reduced variate, y, on the y-axis versus wind speed on the x-axis. This curvature will be curved downwards (i.e. concave) and generally results in a conservative fit (over-estimation) which is further exaggerated upon extrapolation to high return periods like 50 years (y=3.9) and higher.

A possible solution is to precondition the data before fitting the slope and offset. The wind speeds are transformed so that the parent distribution becomes a Weibull with a k-parameter of 1 for which the convergence is extremely fast and thus the Gumbel approximation always very good (Cook, 1982). To achieve this, the wind speeds of the extreme samples are simply raised to the power of k, where k is the parent Weibull distribution. Often k=2 is used as a common assumption in wind energy. In addition using k=2 makes the transformed wind speeds proportional to the dynamic pressure, related to the thrust exerted by the wind. However, the real argument for preconditioning is purely statistical and is illustrated in the graphs below.

Abb. 1. Illustration of the asymptotic nature of the Gumbel model. In the both graphs blue curves show the exact distribution for an annual number of independent samples of N=101 to 107 in steps of 10. Red curves show the Gumbel asymptote assuming N is infinite (hidden behind the blue curves on the right graph).Note that as N increases the blue curves converges to the red. Left graph illustrates the situation for k=2 and the right graph for k=1, which is equivalent to using preconditioning.

Referenzen:

SITE COMPLIANCE & LOAD RESPONSE
SITE COMPLIANCE: Überblick ♦ Schritt-für Schritt ♦ Berechnung ♦ Ergebnisse
Hauptprüfungen: Komplexität ♦ Extremwind ♦ Turbulenz ♦ Windverteilung ♦ Windshear ♦ Neigung der Anströmung♦ Luftdichte
Andere Prüfungen: Erdbebenrisiko ♦ Temperaturbereich ♦ Blitzrate
LOAD RESPONSE: Überblick ♦ Berechnung ♦ WEA-Modelle ♦ Ergebnisse
Anhang: Gumbel Theory of Extremes ♦ Frandsen-Modell ♦ Grenzen in SITE COMPLIANCE ♦ Theorie Ermüdungslasten ♦ Sektormanagement ♦ IEC 61400-1 Ed.2 ♦ IEC 61400-1 Ed.4 ♦ Weiterbetrieb ♦ Siteres ♦ Tropical Cyclone Analysis ♦ Downscaling, Offshore-Modus & Spektralkorrektur