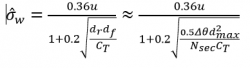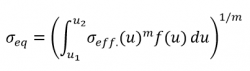Lasten - Anhang II: Frandsen Effective turbulence model

From Wiki-WindPRO
Jump to navigation Jump to search

Zur deutschen Hauptseite | Alle deutschsprachigen Seiten


Der folgende Text beschreibt die wesentlichen Annahmen und Schritte der Implementation des Frandsen-Modells (Effektive Turbulenz-Modell). Die meisten Annahmen sind direkt in der IEC-Richtlinie[1][2] oder in Frandsens eigener Publikation[3] spezifiziert.


Das Frandsen-Modell[1][2][3] definiert die sogenannte Effektive Turbulenz als die Kombination der Umgebungsturbulenz mit der Nachlaufturbulenz der Nachbar-WEA. Dabei werden die Materialeigenschaften so mit einbezogen und über alle Windrichtungen integriert, dass daraus die Akkumulation der Ermüdung abgeleitet werden kann. Gemäß IEC61400-1 Ed. 3 2010[2], wird die Effektive Turbulenz basierend auf dem 90%-Fraktil der Umgebungsturbulenz berechnet.

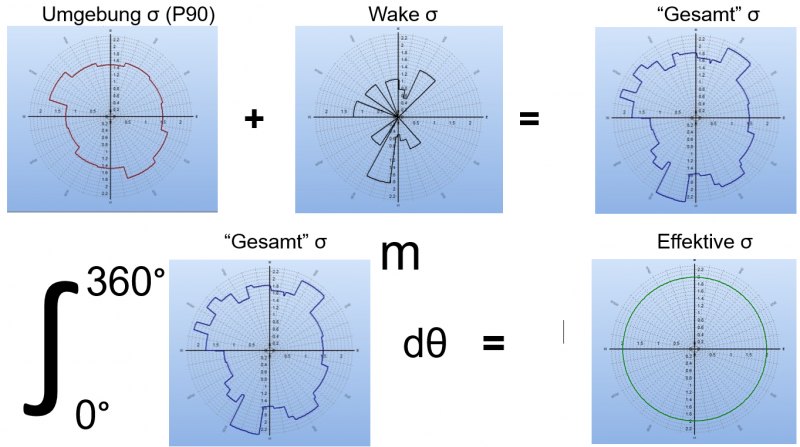
Die Abbildungen zeigen vereinfacht die Berechnungsschritte zur Ermittlung der Effektiven Turbulenz für eine WEA. m ist der Exponent der Wöhlerlinie für das Material.



Für die Berechnung mit dem Frandsen-Modell wird für jede WEA-Position Folgendes benötigt:

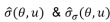  1. - Umgebungsturbulenz (mittel & Standardabweichung abhängig von Windrichtung und Windgeschwindigkeit)
  2. W(Ai,ki) & f(θi) - Sektorweise Häufigkeiten und Weibullverteilungen
  3. CT (WEA-Schubbeiwertskurve) und Parkgeometrie
  4. m - Exponent der Wöhlerlinie (Materialermüdung) für das Material der betrachteten Komponente


1. dient zur Berechnung der charakteristischen Umgebungsturbulenz (90%Fraktil).

2. dient zur Berechnung der sektoriellen Windgeschwindigkeitsverteilung.

3. dient zur Berechnung des Wake-Beitrags zur Turbulenz.

4. wird im ermüdungsgewichteten Kombinationsmodell der einzelnen Richtungen verwendet, um eine omnidirektionale effektive Turbulenz als Funktion der Windgeschwindigkeit zu erhalten.


Eine wichtige Entscheidung im Rahmen der SITE COMPLIANCE-Entwicklung bzgl. Implementation des Frandsen-Modells bestand darin, direkt mit den Standardabweichungen der Windgeschwindigkeit (σ) anstelle der sonst üblichen Turbulenzintensität (TI) zu arbeiten. Für diese Entscheidung gibt es mehrere Gründe. Erstens heißt es in Frandsens Originalpublikation[3] (S. 84) direkt: "Das Modell wird in Form von Standardabweichungen der Windgeschwindigkeitsschwankungen und nicht in Form der Turbulenzintensität ausgedrückt." Zweitens ist eine grundlegende Annahme in Frandsens Modell, dass die Lasten proportional zu σ, der Standardabweichung der Windgeschwindigkeit, sind. Drittens ist die im IEC-Auslegungsgrenzwert ("Normales Turbulenzmodell") angenommene Variation von σ mit der Windgeschwindigkeit linear für (u,σ), aber nicht für (u,TI).

Die Umsetzung des Frandsen-Modells, wie sie in [1][2] beschrieben ist, enthält eine Reihe von Annahmen und Berechnungsschritten. Die wichtigsten Annahmen in der SITE COMPLIANCE-Implementierung sind (die meisten sind direkt in der Norm angegeben[1][2]):

  • "Es wird keine Verringerung der mittleren Windgeschwindigkeit innerhalb des Windparks angenommen" (kein Nachlaufdefizit!)[1][2]
  • Nur Wake der nächsten Nachbar-WEA wird betrachtet, falls sich Wakes überlappen[1][2]
  • Die Turbulenzstrukturkorrektur wird sowohl auf σ als auch auf σσ angewendet.
  • Die Wakes haben eine feste Winkelbreite von 22° unabhängig von der Entfernung[3][4] (alternativ variable Breite einstellbar in SITE COMPLIANCE)


Die wesentlichen Schritte der Berechnung der Effektiven Turbulenz sind:

  • "Gesamt"turbulenz (σT) wird in jeder Richtung berechnet, indem das gemessene 90%-Fraktil der Umgebungsturbulenz (σC) und die berechnete Wake-Turbulenz kombiniert werden (σwake)[1][2] :

wobei

(90%-Fraktil der Umgebungsturbulenz)[5]

und


  • "Effektive Turbulenz" wird aus der "Gesamtturbulenz" hoch m (Wöhlerexponent) berechnet und über alle Richtungen, gewichtet mit ihrer relativen Häufigkeit (f), numerisch integriert:

Das Frandsen-Modell erfordert eine Korrektur für große Windparks, wenn bestimmte Bedingungen erfüllt sind, berücksichtigt aber [1][2] nur den Sonderfall einer regelmäßigen Parkgeometrie. In SITE COMPLIANCE wurde eine allgemeinere, sektorielle Version dieser Korrektur für große Windparks implementiert. Für jeden Sektor wird die folgende Auswertung durchgeführt:

  • Wenn >5 Nachbar-WEA in einem Sektor stehen, ist dieses ein "großer-Windpark-Sektor":
    • In direkter Nachlaufrichtung wird σT berechnet wie oben (keine Korrektur der Umgebungsturbulenz)[1][2]
    • In Richtungen ohne Wake (>10RD), wird die Umgebungsturbulenz σc angepasst über [1][2]:

wobei

Der letztgenannte Bruch auf der rechten Seite in der obigen Gleichung wurde in [4] als eine allgemeinere Version des Bruches auf der linken Seite vorgeschlagen, der in der Norm explizit angegeben ist und nur regelmäßige Park-Geometrie abdeckt. Das Argument unterhalb der Wurzel stellt “Fläche zu Schub” dar. Im Term auf der rechten Seite ist die regelmäßige Park-Geometrie durch eine Winkelabhängigkeit ersetzt mit der Fläche eines "Tortenstücks" A=0.5Δθd2max. Nsec ist die Anzahlder WEA innerhalb des "Tortenstücks" oder Sektors, dmax der Radius des Tortenstücks und damit der Abstand zur entferntesten Nachbar-WEA innerhalb des Sektors.


Berechnung der Äquivalenten Effektiven Turbulenz (nicht Teil der IEC-Richtlinie)

Diese Berechnung ist nicht Teil der IEC-Norm, sondern basiert auf Überlegungen, die in Frandsens Originalarbeit vorgestellt wurden [3]. Die Äquivalente Effektive Turbulenz wird zur Entscheidung genutzt, wann die berechnete effektive Turbulenz die IEC-Auslegungsgrenze überschreitet, um zu beurteilen, ob diese Überschreitung kritisch ist oder nicht. Die Hauptannahme ist die gleiche wie beim Frandsen-Modell, aber es wird ein zusätzlicher Berechnungsschritt hinzugefügt: die Integration der effektiven Turbulenz über alle relevanten Windgeschwindigkeiten, während das Frandsen-Modell nur über die Richtungen integriert. Diese zweite Integration über die Windgeschwindigkeiten setzt voraus, dass die Sensitivität der WEA gegenüber Windgeschwindigkeitsschwankungen für den relevanten Windgeschwindigkeitsbereich konstant ist, was eine deutliche Erweiterung zur Annäherung des Frandsen-Modells darstellt. Die Äquivalente Effektive Turbulenz wird wie folgt berechnet:

Dabei ist m der Wöhler-Exponent, f(u) ist die Häufigkeit der Windgeschwindigkeitsklasse (omnidirektional) und σeff.(u) die Effektive Turbulenz in Abhängigkeit von der Windgeschwindigkeitsklasse, d.h. das Ergebnis der Effektiven Turbulenz-Berechnung gemäß Frandsen-Modell.

Das Ergebnis der Effektiven Turbulenz für eine bestimmte WEA wird mit der IEC-Auslegungsgrenze für die WEA-Klasse verglichen, indem die Äquivalente Effektive Turbulenz für die gewählte IEC-Auslegungsklasse (Turbulenz und Häufigkeit) und für die tatsächlichen WEA-Positionen berechnet wird. Die tatsächliche WEA-Ergebnisse werden auf das Ergebnis für die IEC-Klasse normalisiert. Wenn das normalisierte Ergebnis (Verhältnis) größer als 1 ist, wird die IEC-Überschreitung als kritisch angesehen. Die Integrationsgrenzen werden so gesetzt, dass sie mit dem IEC-Prüfintervall übereinstimmen.


Referenzen:

  1. ↑ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 IEC 61400-1 ed. 3, 2005, Wind turbines – Part 1: Design requirements
  2. ↑ 2.00 2.01 2.02 2.03 2.04 2.05 2.06 2.07 2.08 2.09 2.10 IEC 61400-1 ed. 3, 2010, Amendment 1
  3. ↑ 3.0 3.1 3.2 3.3 3.4 Frandsen, S. T., 2007, Turbulence and turbulence generated loading in wind turbine clusters, Risø report R-1188
  4. ↑ 4.0 4.1 Nielsen, M., Jørgensen, H. E. and Frandsen, S. T., 2009, Wind and wake models for IEC 61400-1 site assessment, Proceedings of the European Wind Energy Conference (EWEC 2009)
  5. ↑ Für komplexes Gelände σC multipliziert mit dem Turbulenzstrukturkorrektur-Parameter, CCT


SITE COMPLIANCE & LOAD RESPONSE
SITE COMPLIANCE: Überblick ♦ Schritt-für Schritt ♦ Berechnung ♦ Ergebnisse
Hauptprüfungen: Komplexität ♦ Extremwind ♦ Turbulenz ♦ Windverteilung ♦ Windshear ♦ Neigung der Anströmung♦ Luftdichte
Andere Prüfungen: Erdbebenrisiko ♦ Temperaturbereich ♦ Blitzrate
LOAD RESPONSE: Überblick ♦ Berechnung ♦ WEA-Modelle ♦ Ergebnisse
Anhang: Gumbel Theory of Extremes ♦ Frandsen-Modell ♦ Grenzen in SITE COMPLIANCE ♦ Theorie Ermüdungslasten ♦ Sektormanagement ♦ IEC 61400-1 Ed.2 ♦ IEC 61400-1 Ed.4 ♦ Weiterbetrieb ♦ Siteres ♦ Tropical Cyclone Analysis ♦ Downscaling, Offshore-Modus & Spektralkorrektur
Retrieved from "http://help.emd.dk/mediawiki/index.php?title=Lasten_-_Anhang_II:_Frandsen_Effective_turbulence_model&oldid=17098"